Basically on Friday our class did a worksheet on Investigating Rules of Differentiation. The worksheet allowed us to do a couple of problems to see if we noticed any patterns. Afterwards we learned some rules that can be very useful for the “Definition of the Derivative”. The rules are as follows:
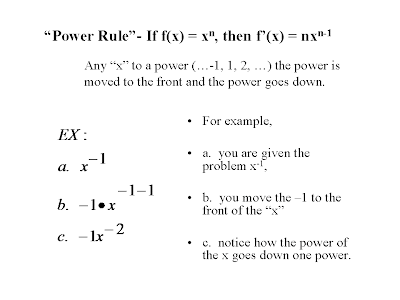
After we learned the three basic rules, we went deeper into the pool of derivatives and investigated more problems. Notice how each rule was used to solve other problems (multiple rules in one problem). Next we then applied the three basic rules already learned to the next three rules. More Rules: 
So those are all the rules we’ve learned so far. I wasn't sure how to put put images on, i couldn't find paint but I hope these explanations help…don't let those carrots confuse you or Laura's engergizer bunny will eat them. That made no sense.
Hold on, I'm not done yet, we are going to have a test on Tuesday, September 9 on the Summer Packet. The homework was page 120 # 1-23 odd. Enjoy and happy break.
5 comments:
On the Quotient Rule, shouldn't there be parentheses? -
If f(x) = u / v, then f’(x) = (v * u’ - u * v’) / v^2
Go Christine! Way to be the first scribe.
“Power Rule”- If f(x) = x^n, then f’(x) = nx^n-1
Ex: x^-1 = -1x, any “x” to a power (…-1, 1, 2, …) the power is moved to the front and the power goes down. For the above example, you are given the problem x^-1, you move the –1 to the front of the “x” and notice how the power of the x goes down one power.
This brings up a question I was pondering; isn't it -1X^-2? I believe the shortcut equation is NX^N-1. N being the power, shouldn't it be -1X^(-1) - 1, therefore inducing a -2?
Well done Christine, that's a lot of mathy language to putting up through microsoft word or just this scanty HTML formatting system they seem to enjoy.
The only thing I really have to comment on is that I would have preferred if the mathy sections were separate from the text sections. At the same time, I understand the difficulty behind including as many examples as you did, and appreciate its merit. It all seemed a bit jumbled, however, but beyond that it was excellently written. Great work!
To answer Dalton, I think (and Jake and Peter can laugh at me for even attempting this) that if f(x) = x^-1, then it's actually f'(x) = -x^-2. I think that's what you meant, and just dropped a sign. Oh well.
Other than that, I can only say that I agree with Alex: I wonder if it's possible to differentiate between the text and the formulas, even if it's just by bolding the formulas, just to make it a little clearer. I also feel like someone should figure out the HTML jargon for how to do a superscript, because the karats (carats, carrots) bother me. But that's a little picky. Good job, Christine.
Awesome job Christine!
In response to Caroline, to superscript stuff you use sup (with the triangle parenz), but the problem is, as Christine might have discovered, this blogger doesn't accept that HTML tag. Does anyone know of any other ways to format HTML? On the other hand, I really don't think the carrots are that annoying, so I wouldn't spend too much time worrying about it (sorry Caroline).
I would say somehting useful/interesting/helpful about the math, but I don't really have anything to say that the other 4 didn't comment on - so I'll just say I agree with Alex and again, great job Christine!
Post a Comment