Implicit Differentiation
An example of a function that is explicitly defined would be y=f(x).
But unfortunately not all functions are explicitly defined, such as the equation of a circle x^2 + y^2 = r^2. This is an example of a function that is implicitly defined. Often with implicitly defined functions it is not possible to solve for y.
To equation of a circle can be divided into two pieces: the top half of the circle and the bottom half of the circle, with
each piece a separate function
The Implicit Differentiation Process
1. Differentiate both sides of the equation with respect to x
2. Collect the terms with dy/dx on one side of the equation
3. Factor out dy/dx
4. Solve for dy/dx
example 1:
x^3 + y^3 - 9xy = 0
The graph of x^3 + y^3 - 9xy = 0, a folium
-This function has well defined tangent lines at every point on the graph.
-Even though it is not a function in the classic sense, it is still differentiable
-The derivative from the right = the derivative from the left
x^3 + y^3 -9xy = 0
3x^2 + 3y^2 * dy/dx - 9x*dy/dx -9y = 0 Since y is a function of x, when taking the derivative of any term with y,
multiply by dy/dx
3y^2*dy/dx - 9x*dy/dx = 9y - 3x^2
y^2*dy/dx - 3x*dy/dx = 3y - x^2
dy/dx( y^2 - 3x ) = 3y -x^2
dy/dx = (3y - x^2)/(y^2 -3x)
*can use notation y' or dy/dx
example 2:
2y = x^2 + siny
2*y' = 2x + cosy*y'
2*y' - cosy*y' = 2x
y'( 2 - cosy) = 2x
y' = 2x / (2 - cosy)
Finding the tangent and normal lines to a curve:
-to find the slope of the tangent at a point, plug the coordinates of the point into the equation for dy/dx
example 1:
x^2 - xy + y^2 = 7 at ( -1,2 )
2x - x*dy/dx - y + 2y*dy/dx = 0
-x*dy/dx + 2y*dy/dx = y - 2x
dy/dx ( 2y-x ) = y -2x
dy/dx = ( y- 2x )/( 2y-x )
dy/dx(-1,2) = (2 - 2* -1)/(2*2 + 1) = 4/5
tangent: y-2 = 4/5(x+1)
normal: y-2 = -5/4(x+1)
*To find slope of normal line, use opposite inverse of slope of tangent line
In class, we took our first homework quiz over the derivatives thus far, with the exception of the exponential and logarithmic derivatives
Homework: page 155# 3-28, multiples of 3
Wednesday, September 26, 2007
Implicit Differentiation
Tuesday, September 18, 2007
More Derivation Rules
A mathematician went insane and believed that he was the differentiation operator. His friends had him placed in a mental hospital until he got better. All day he would go around frightening the other patients by staring at them and saying "I differentiate you!"
One day he met a new patient; and true to form he stared at him and said "I differentiate you!", but for once, his victim's expression didn't change.
Surprised, the mathematician marshalled his energies, stared fiercely at the new patient and said loudly "I differentiate you!", but still the other man had no reaction. Finally, in frustration, the mathematician screamed out "I DIFFERENTIATE YOU!"
The new patient calmly looked up and said, "You can differentiate me all you like: I'm e to the x."
http://www.onlinemathlearning.com/math-jokes-calculus.html
Homework: Page 172, #1-11

Sunday, September 16, 2007
Chain Rule, Motion along a line, and R.O.C. of the Area of a circle with respect to the Radius.
-The formula for the are of a circle is A= πr^2
-Using the power rule, take the derivative of A= πr^2. to get dA/dr= 2πr.
Example:
When R=5
dA/dr=2π5= 10π
Motion Along a Line:
-This is the relationship between position, velocity, and acceleration.
-Position: Where an object is with respect to time. S(t)
-Velocity: Is measured by both the magnitude and direction. V(t)=S'(t)
-Acceleration: Change in velocity with respect to time. A(t)=V'(t)=S"(t)
Example:
A rock (named ethan) is shot straight up into the air with a velocity of 160ft/sec. Using the equation S=160t-16t^2. A)Find how high ethan goes. B)How long it takes ethan to reach the vertex. C) Find the time when ethan is at 256 feet above the ground. D) Find the speed of ethan when it is 256 feet above the ground. E) Find the acceleration of ethan.
A) S=160t-16t^2
S=160•
S=400 feet.
B) First take the derivative of original equation which= ds/dt=160-32t. Then simply set the equation equal to zero.
160-32t=0
t=5 seconds
C)256=160t-16t^2
16t^2-160t+256=0
t^2-10t+16=0
(t-8)(t-2)=0
At time=8 seconds and time=2 seconds ethan will reach 256 feet.
D) To find the speed at those previous points, use the velocity equation.
V(8)= 160-32•
V(8)=-96 ft/s
V(2)=160-32
V(2)=96ft/s
E) To find the acceleration take the derivative of the velocity equation.
a(t)=V'(t)= -32 ft/sec
Chain Rule
This rule is used to take the derivative of a function when that function, according to Mr. Marchetti, "is very ugly."
Chain Rule: dy/du=(dy/du)•(du/dx)
Example:
f(x)=(3x+5)^10
-First take the derivative of the "inside equation" which is u=3x+5, the derivative of that then equals du/dx=3
-Then take the derivative of the "outside equation" which is y=u^10 the derivative of that then equals dy/du=10u^9
-Then simply place those derivatives into the chain rule equation to get 10(3x+5)•3
Homework Due Tuesday September 18: Pg 129, #2,4,9,12,14,16,25 and pg 146 #1-19 odd
Thursday, September 13, 2007
graphing nDeriv(, IVT, RoC
So, it appears as if I chose a good day to have the most siblings/step-siblings of all of you, and if any of you were hiding anything, it's your loss.
As it turns out, we didnt go over much in class, mostly just how to graph a numerical derivative using our calculator, the IVT (Intermediate Value Theorem), and Rates of Change. Based on the fact that I spaced making this post until the night before class, I won't have time to download the software and do the whole screenshot deal, but it's a nice thought. Use your imaginations.
GRAPHING THE NUMERICAL DERIVATIVE:
1. Input the funtion of which you wish to see the derivative into the Y1 entry line.
2. In the Y2 entry line, follow the following (teehee!) progression of buttons:
MATH
8
VARS
→Y-VARS
1
1
,
X
,
X
)
3. Now that you have punched this in, hit the ENTER button. On the resultant graph, you now have the original function and its derivative.
4. Note: When you see in the Y2 entry line “nDeriv(Y1,X,X)” I suppose you may want to know what this all means. This means you are finding the numerical derivative of the Y1 function for the variable X in terms of X. Instead of using nDeriv( to find an individual slope at a point, we are instead using it to graph the slopes of all tangent lines to the curve, THE DERIVATIVE!
INTERMEDIATE VALUE THEOREM
The Intermediate Value Theorem is stated as follows:
If a and b are any two values on a function, f, and f is differentiable then f’ takes on all values between f’(a) and f’(b).
As Marchetti said, that’s a lot of mathspeak, which is something most of us don’t understand. Basically, if a function is differentiable, then a tangent line exists at all points. If I’m wrong on that, then correct me. Basically, it says that if the function can have a derivative between a and b, then the function will.
Rates of Change:
There are two methods for finding Instantaneous RoC, finding the RoC for any point on the function, and finding the RoC at a specific point. Here they are:
Inst. RoC for a Function (Defn. of Derivative):
f'(x)=(f(x+h) - f(x))/h
Inst. RoC at a Point, “a”
f'(a)=(f(a+h) - f(a))/h
I think that’s about it, thank you all for your time and I apologize dearly for my lack of punctuality. The homework, in case you’re looking desperately at this, is pg 140 # 29, 28, 33, 31, and 32 (yes, in that order).
Wednesday, September 12, 2007
Ok, I'm encoding this post in HTML so let me know if there are any problems. I figure I can use some coding to slightly alter the color of the math portions, therefore making them easier to read. Alright, so here we go:
Graph of Y' Stuff
Graphs are pretty important in Calculus as they form an easy allabi when you can't solve a problem. Anyways, there are alot of sweet things to know about a graph for example, if we take the function F(x)=X2 who's graph is
then you take the Derivative of the function, which happens to be Y' = 2X1 and you get this
Now you'll notice several things right away. First, is that the degree of the function is one lower. Second, you'll also notice, and the zero of the derivative is at the minimum of the original function. This can clearly be seen when you graph both of them at the same time
and zoomed in
Example Graphs
I figure I'll use a list instead of a table, the blog site probably won't respond to the coding. The function is in black, whilst the derivative is in red. The original function will come first, then both of then together.
So if we can take two rules from all of this:
- If F(x) is a polynomial, than F'(x) will be one degree lower.
- If F(x) is continuous and at a maximum or a minimum at A than F'(x) will be 0 at A.
Trig Tricks
Alright, even though Trigonometry is a total pain in the ass, we still have to do it. That being said, it's time consuming, stressful, and slightly annoying when you're attempting to find the F'(x) of a trig function. So, there are a couple tricks that make your life a whole lot easier when applied with the other calculus rules. On the left is a function, and on the right in green is the Y' of that function
- F(x)=sinX F'(x)=cosX
- F(x)=cosX F'(x)=-sinX
- F(x)=secX F'(x)=secXtanX
- F(x)=tanX F'(x)=sec2X
- F(x)=cscX F'(x)=-cscXcotX
- F(x)=cotX F'(x)=-csc2X
Below is an example problem of how to use these tricks along with the Quotient Rule:
Your starting function
Y=cosX / (1-sinX)
Apply the Quotient Rule
Y'= (1-sinX)(-sinX) - cosX(-cosX) / (1-sinX)2
Simplify by distributing
Y'=-sinX + sin2X + cos2X / (1 - sinX)2
Next use identies to turn the Sin2X into (1-cos2X) and subtract the cos2X
Y'= -sinX + 1 + -
Now cancel out a (1 - sinX)
Y'=
Y'= 1 / (1 - sinX)
- Alright, that's it
- Dalton King
Saturday, September 8, 2007
9/7/07
Sometimes Limits Don't Exist
Provided the limit exists, the definition of a derivative is

However, the limit might fail to exist in four conditions:
1. Corner – one-sided derivatives are different
2. Cusp – the slopes of the secant lines approach ∞ from one side and –∞ from the other
3. Vertical tangent – the slopes of the secant lines approach either ∞ or –∞ from both sides
4. Discontinuity
For examples of what each of these conditions look like, see pages 105-106 in the textbook.
Don’t worry about this until it comes up in problems – you can still take the derivative of the equations!
Differentiability
Differentiability implies two things, which will become more important later:
1. Local Linearity
Graph a function, say y=(x-2)² + 4. Zoom in a lot on one area of this parabola and it looks linear. 2. Local continuity
Data
If you are given a table of values instead of an equation, you can still estimate the derivative of the midpoint between two data points by finding the average rate of change using (y2-y1)/(x2-x1) between the two points.
To see an example of this, refer to pages 99-100 in the textbook. First, they made a scatter plot of Table 3.1 (Figure 3.6) Next, they found the average rate of change and midpoint between the first two points, the 2nd and 3rd points… This is in Table 3.2. The midpoint became the x value and the average rate of change became the y value when they made a graph of the derivative (see page 100).
Numerical Derivatives
This is a calculator trick so that you don’t have to go through all the steps to find the slope of a tangent line.
On the calculator, press MATH then 8:nDeriv(. Fill in the equation, the variable that you want to take the derivative with respect to, and the value given in the problem.Ex. Given y=x³-3x²+4, find the tangent line at x=1. You can press nDeriv(x³-3x²+4,x,1) and get -2.999 which you would round to -3.To do this without a calculator, find the derivative of the equation which in the above example is y’=3x²-6x. Plug the x value into this equation to find the slope y’(1)=3(1)²-6(1)=–3.
If you want to find the y intercept of the equation of the tangent line, you would first plug 1 in the original equation to find f(x) which is f(1)=2. Then use this point (1,2) which you know is on the tangent line, along with the slope you found previously to solve for b.2=–3(1)+b → 5=b Therefore, the equation of the tangent line is y=–3x+5.
Homework Due Tuesday
Worksheet - 1-19 odd (front page) - just apply the rule, don't simplify.
Pg. 101 - exercises 7-12, 15, 17-19, 26
Pg. 111 - 1-10, 11-21 odd
Pg. 120 - 27, 29, 31
Monday, September 3, 2007
Investigating Rules of Differentiation from Friday, Aug 31
Basically on Friday our class did a worksheet on Investigating Rules of Differentiation. The worksheet allowed us to do a couple of problems to see if we noticed any patterns. Afterwards we learned some rules that can be very useful for the “Definition of the Derivative”. The rules are as follows:
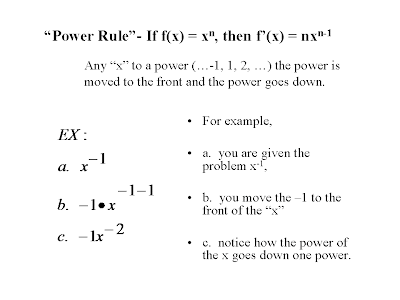


 After we learned the three basic rules, we went deeper into the pool of derivatives and investigated more problems. Notice how each rule was used to solve other problems (multiple rules in one problem). Next we then applied the three basic rules already learned to the next three rules. More Rules:
After we learned the three basic rules, we went deeper into the pool of derivatives and investigated more problems. Notice how each rule was used to solve other problems (multiple rules in one problem). Next we then applied the three basic rules already learned to the next three rules. More Rules: 


So those are all the rules we’ve learned so far. I wasn't sure how to put put images on, i couldn't find paint but I hope these explanations help…don't let those carrots confuse you or Laura's engergizer bunny will eat them. That made no sense.
Hold on, I'm not done yet, we are going to have a test on Tuesday, September 9 on the Summer Packet. The homework was page 120 # 1-23 odd. Enjoy and happy break.











