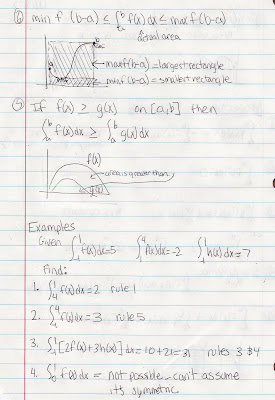Hi Everyone!
This Friday (11/30) is food day! Please bring whatever you decided you were going to because otherwise we'll all be sad (and hungry).
Homework: pg. 274 #'s 1-33 odd
We took lots of notes today - here are scanned copies (to enlarge click on them).
Wednesday, November 28, 2007
Monday, November 5, 2007
Newton's Method , Differentials, Related Rates
Hi guys
we have Quiz on Nov 6th, Tuesday.
Newton's Method
The general method

If our first guess was a good one, the approximate solution
was a good one, the approximate solution should be an even better approximation to the solution of
should be an even better approximation to the solution of  . Once we have
. Once we have  , we can repeat the process to obtain
, we can repeat the process to obtain  , the solution to the linear equation
, the solution to the linear equation

Solving in the same way, we see that

Maybe now you see that we can repeat this process indefinitely: from , we generate
, we generate and so on. If, after n steps, we have an approximate solution
and so on. If, after n steps, we have an approximate solution , then the next step is
, then the next step is

Provided we have started with a good value for , this will produce approximate solutions to any degree of accuracy.
, this will produce approximate solutions to any degree of accuracy.
Dfferentials

Note that if we are just given then the differentials are the df and dx and we compute them the same manner
then the differentials are the df and dx and we compute them the same manner
2x (dx/dt) + 2y (dy/dt) = 0
we have Quiz on Nov 6th, Tuesday.
Newton's Method
The general method
More generally, we can try to generate approximate solutions to the equation  using the same idea. Suppose that
using the same idea. Suppose that  is some point which we suspect is near a solution. We can form the linear approximation at
is some point which we suspect is near a solution. We can form the linear approximation at  and solve the linear equation instead.
and solve the linear equation instead.
That is, we will call the solution to  . In other words,
. In other words,

If our first guess
 was a good one, the approximate solution
was a good one, the approximate solution should be an even better approximation to the solution of
should be an even better approximation to the solution of  . Once we have
. Once we have  , we can repeat the process to obtain
, we can repeat the process to obtain  , the solution to the linear equation
, the solution to the linear equation
Solving in the same way, we see that

Maybe now you see that we can repeat this process indefinitely: from
 , we generate
, we generate and so on. If, after n steps, we have an approximate solution
and so on. If, after n steps, we have an approximate solution , then the next step is
, then the next step is
Provided we have started with a good value for
 , this will produce approximate solutions to any degree of accuracy.
, this will produce approximate solutions to any degree of accuracy.Dfferentials
Given a function  we call dy and dx differentials and the relationship between them is given by
we call dy and dx differentials and the relationship between them is given by
Note that if we are just given
Related Rates
There is 13ft of string beteen two people. The people holding the string.
One person(x) is moving left and another person (Y)is moving forward. (keeping the distance between people 13ft)
speed of Y person is 4ft/s
We can know that the length of x side is 5ft and length of y side is 12ft to use pythagorean theaorem.
2 2 2
x + y = 13
2x (dx/dt) + 2y (dy/dt) = 0
x(dx/dt) + y(dy/dt) = 0
x(dx/dt) + y*4 = 0
5(dx/dt) + 12*4 = 0
dx/dt = - 9.6
Subscribe to:
Comments (Atom)