Area Under A Curve

Sorry this is late, but we had this lesson on Wed, Nov 27, 2007

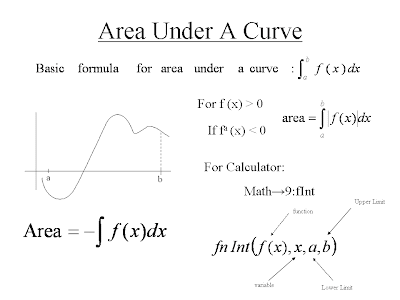
For some practice problems, go to page 264 and do Exploration 1
Homework: pg 254 #5-13 odd, 20; pg 267 #7-41 odd

Integrals

Hi Everyone!
This Friday (11/30) is food day! Please bring whatever you decided you were going to because otherwise we'll all be sad (and hungry).
Homework: pg. 274 #'s 1-33 odd
We took lots of notes today - here are scanned copies (to enlarge click on them).

Newton's Method , Differentials, Related Rates

Hi guys
we have Quiz on Nov 6th, Tuesday.

Newton's Method
The general method

More generally, we can try to generate approximate solutions to the equation using the same idea. Suppose that is some point which we suspect is near a solution. We can form the linear approximation at and solve the linear equation instead.
That is, we will call the solution to . In other words,

If our first guess was a good one, the approximate solution should be an even better approximation to the solution of . Once we have , we can repeat the process to obtain , the solution to the linear equation

Solving in the same way, we see that

Maybe now you see that we can repeat this process indefinitely: from , we generate and so on. If, after n steps, we have an approximate solution , then the next step is

Provided we have started with a good value for , this will produce approximate solutions to any degree of accuracy.


Dfferentials

Given a function we call dy and dx differentials and the relationship between them is given by

Note that if we are just given then the differentials are the df and dx and we compute them the same manner

Related Rates

There is 13ft of string beteen two people. The people holding the string.

One person(x) is moving left and another person (Y)is moving forward. (keeping the distance between people 13ft)

speed of Y person is 4ft/s

We can know that the length of x side is 5ft and length of y side is 12ft to use pythagorean theaorem.

2 2 2

x + y = 13

2x (dx/dt) + 2y (dy/dt) = 0

x(dx/dt) + y(dy/dt) = 0

x(dx/dt) + y*4 = 0

5(dx/dt) + 12*4 = 0

dx/dt = - 9.6

Mean Value Theorem Applications, First Derivative Test

So this is Jake. Basically, Mr. Marchetti extrapolated on the Mean Value Theorem (grrr theorem). Anyways, the homework he gave us was page 192 # 1-13 odd, 19-37 odd, 42, and 43. Also, he postponed the quiz until Tuesday the 23rd, so cram for that while you're at it.

Now, the MVT (Mean Value Theorem) has 3 basic premises that apply.
1. The Increasing/Decreasing Rule
So this rule basically states that, and I quote, "If, over the course of the interval, the secant line's slope is positive, then the tangent line's slope will also be positive."
In literal terms, this means that when the function is increasing, the secant line, and therefore the tangent line's slopes will be positive.



What this means to us is that functions increase when f'(x) > 0 and they decrease when f'(x) <0

The second rule is that a line with a derivative of zero is constant, so x=5 is just a horizontal line.

The third rule of the MVT is that "3. Functions with the same derivative only differ by a constant." Therefore, if f'(x) = g'(x), then f(x) = g(x) + constant
Here is an example for you: we have both f'(x) and g'(x) equaling 2x
You know that f(x) must = x^2 and that g(x) must also = x^2. However, g(x) could also equal x^2 + 121. That would still result in a derivative of 2x, the same as for f'(x), proving that functions with identical derivatives only differ by a constant.

Now that we have the MVT explained, we can move onto the First Derivative Test. What this rule states is that "When the derivative goes from positive to negative, you have a max. When the derivative goes from negative to positive, you have a min. And finally, if the derivative doesn't change signs, then there is no max or min." Pretty self-explanatory.

In this graph right here, you can see that, at -2, the derivative is negative and then switches to positive. This shows that there is a relative minimum at that point. At -1, the derivative is positive and goes to negative, leading there to be a maximum at that point.

To put all of this together, there is a good example that Mr. Marchetti showed to us on the board. You have the function y= x^3 - 4x. You need to find the maximum(s) and minimum(s). Ready go. So to solve this, you need to first find the equation's derivative. That is y' = 3x^2 - 4. You make that equation equal to 0 in order to determine where the critical points are in this specific function.
0 = 3x^ - 4
4 = 3x^2
4/3 = x^2
+/- (4/3)^.5 = x (this would be a lot less cluttered if I could insert stuff...)
+/- 2 / (3)^.5 = x

Now that you have the critical points of the function (where the derivative changes signs, which results in a max or a min as stated in the First Derivative Test), you can figure out how the function's derivative behaves in each interval. The intervals that you will have in this instance will be (- infinity, -2/(3)^.5), (-2/(3)^.5, 2/(3)^.5), and (2/(3)^.5, infinity). What you do is pick any value within each interval and plug that into the derivative equation that you found earlier (3x^2 - 4) to find how the derivative in that interval behaves. Remember, the endpoints of each interval are 0's, so the derivative crosses the x axis at those points and changes signs.
(- infinity, -2/(3)^.5)...: 3(-5)^2 - 4 = 71, positive in this interval
(-2/(3)^.5, 2/(3)^.5)...: 3(0)^2 - 4 = -4, negative in this interval
(2/(3)^.5, infinity)...: 3(5)^2 - 4 = 71, positive in this interval
now, to find which of these critical points is the maximum and which is the minimum, you refer again to the First Derivative Test. It states that when the derivative goes from positive to negative, you have a maximum. Therefore, at the point -2/(3)^.5), you have a maximum. Also, because the First Derivative Test states that when the derivative goes from negative to positive, you have a minimum, you know that your minimum is at 2/(3)^.5.

That is all that was talked about in class on Wednesday. Again, we'll see if the inserting pictures problem resolves itself or not.

SCRIBE POST - OCTOBER 10, 2007

Hi guys, it's Devon. I was the scribe last Wednesday (October 10). It was a late start day, so all we covered was something called The Mean Value Theorem. We recieved a review packet, and we had to start working on that in preperation for our quiz Friday, October 19th.

Ok. Here we go.

The Mean Value Theorem connects the average rate of change and instantaneous rate of change of a function. The theorem states that all continuous and differentiable points between A and B on a differentiable curve, have at least one tangent line parallel to AB.



Between points A and B, we find a point C. Point C is the point of a parallel tangent line, and can be found by the previous equation.

A graph that represents The Mean Value Theorum would look like this:



An example of this would be driving. If you went on a 3 hour trip, averaging about 30 miles/hour, The Mean Value Theorem states that you would have to be going exactly that speed at least one time in the duration of your drive. That's basically it, it's pretty simple.

Derivatives of Logs and Exponents + Logarithmic Differentiation

I do not have powerpoint so everything is done on word.

The information is on the pictures.

Implicit Differentiation

Implicit Differentiation

An example of a function that is explicitly defined would be y=f(x).

But unfortunately not all functions are explicitly defined, such as the equation of a circle x^2 + y^2 = r^2. This is an example of a function that is implicitly defined. Often with implicitly defined functions it is not possible to solve for y.
             
            To equation of a circle can be divided into two pieces: the top half of the circle and the bottom half of the circle, with         
            each piece a separate function 

The Implicit Differentiation Process
      1. Differentiate both sides of the equation with respect to x
      2. Collect the terms with dy/dx on one side of the equation
      3. Factor out dy/dx
      4. Solve for dy/dx

example 1:  

               x^3 + y^3 - 9xy = 0   

The graph of x^3 + y^3 - 9xy = 0, a folium


                                                       
-This function has well defined tangent lines at every point on the graph. 
-Even though it is not a function in the classic sense, it is still differentiable
-The derivative from the right = the derivative from the left

x^3 + y^3 -9xy = 0 

3x^2 + 3y^2 * dy/dx - 9x*dy/dx -9y = 0           Since y is a function of x, when taking the derivative of any term with y,              
                                                                           multiply by dy/dx   
3y^2*dy/dx - 9x*dy/dx = 9y - 3x^2

y^2*dy/dx - 3x*dy/dx = 3y - x^2

dy/dx( y^2 - 3x ) = 3y -x^2

dy/dx = (3y - x^2)/(y^2 -3x)



*can use notation y' or dy/dx


example 2: 
                         2y = x^2 + siny

2*y' = 2x + cosy*y'

2*y' - cosy*y' = 2x

y'( 2 - cosy) = 2x

y' = 2x / (2 - cosy)


Finding the tangent and normal lines to a curve:
      -to find the slope of the tangent at a point, plug the coordinates of the point into the equation for dy/dx


example 1:
                         x^2 - xy + y^2 = 7  at ( -1,2 )



2x - x*dy/dx - y + 2y*dy/dx = 0

-x*dy/dx + 2y*dy/dx = y - 2x

dy/dx ( 2y-x ) = y -2x

dy/dx = ( y- 2x )/( 2y-x )

dy/dx(-1,2) = (2 - 2* -1)/(2*2 + 1) = 4/5

tangent: y-2 = 4/5(x+1)
normal: y-2 = -5/4(x+1)        
*To find slope of normal line, use opposite inverse of slope of tangent line


In class, we took our first homework quiz over the derivatives thus far, with the exception of the exponential and logarithmic derivatives

Homework: page 155# 3-28, multiples of 3













            






              

                

More Derivation Rules

I hope everyone knew (and still know) rules for Trig Functions, because we took a quiz on the last week or so today, and if you didn't you missed a good 30-40% of the problems. Whoops. Anyway, we continued Rules today with Inverse Trig Functions and Logarithms/Exponential Functions. They are as follows:

Inverse Trig Functions:

Logarithms/Exponential Functions:

On that note:

Marchetti in 9 Months:
A mathematician went insane and believed that he was the differentiation operator. His friends had him placed in a mental hospital until he got better. All day he would go around frightening the other patients by staring at them and saying "I differentiate you!"
One day he met a new patient; and true to form he stared at him and said "I differentiate you!", but for once, his victim's expression didn't change.
Surprised, the mathematician marshalled his energies, stared fiercely at the new patient and said loudly "I differentiate you!", but still the other man had no reaction. Finally, in frustration, the mathematician screamed out "I DIFFERENTIATE YOU!"
The new patient calmly looked up and said, "You can differentiate me all you like: I'm e to the x."
http://www.onlinemathlearning.com/math-jokes-calculus.html

Yeah, I'm a nerd.

Homework: Page 172, #1-11

I didn't want to draw a picture. Sorry.

Chain Rule, Motion along a line, and R.O.C. of the Area of a circle with respect to the Radius.

R.O.C. of the area of a circle with respect to the radius:
-The formula for the are of a circle is A= πr^2
-Using the power rule, take the derivative of A= πr^2. to get dA/dr= 2πr.

Example:
When R=5
dA/dr=2π5= 10π

Motion Along a Line:
-This is the relationship between position, velocity, and acceleration.
-Position: Where an object is with respect to time. S(t)
-Velocity: Is measured by both the magnitude and direction. V(t)=S'(t)
-Acceleration: Change in velocity with respect to time. A(t)=V'(t)=S"(t)

Example:
A rock (named ethan) is shot straight up into the air with a velocity of 160ft/sec. Using the equation S=160t-16t^2. A)Find how high ethan goes. B)How long it takes ethan to reach the vertex. C) Find the time when ethan is at 256 feet above the ground. D) Find the speed of ethan when it is 256 feet above the ground. E) Find the acceleration of ethan.

A) S=160t-16t^2
S=160• 5-16•5^2
S=400 feet.

B) First take the derivative of original equation which= ds/dt=160-32t. Then simply set the equation equal to zero.
160-32t=0
t=5 seconds

C)256=160t-16t^2
16t^2-160t+256=0
t^2-10t+16=0
(t-8)(t-2)=0
At time=8 seconds and time=2 seconds ethan will reach 256 feet.

D) To find the speed at those previous points, use the velocity equation.
V(8)= 160-32•8
V(8)=-96 ft/s
V(2)=160-32•2
V(2)=96ft/s

E) To find the acceleration take the derivative of the velocity equation.
a(t)=V'(t)= -32 ft/sec

Chain Rule
This rule is used to take the derivative of a function when that function, according to Mr. Marchetti, "is very ugly."

Chain Rule: dy/du=(dy/du)•(du/dx)

Example:
f(x)=(3x+5)^10

-First take the derivative of the "inside equation" which is u=3x+5, the derivative of that then equals du/dx=3
-Then take the derivative of the "outside equation" which is y=u^10 the derivative of that then equals dy/du=10u^9
-Then simply place those derivatives into the chain rule equation to get 10(3x+5)•3

Homework Due Tuesday September 18: Pg 129, #2,4,9,12,14,16,25 and pg 146 #1-19 odd

graphing nDeriv(, IVT, RoC

Greetings Kids!

So, it appears as if I chose a good day to have the most siblings/step-siblings of all of you, and if any of you were hiding anything, it's your loss.

As it turns out, we didnt go over much in class, mostly just how to graph a numerical derivative using our calculator, the IVT (Intermediate Value Theorem), and Rates of Change. Based on the fact that I spaced making this post until the night before class, I won't have time to download the software and do the whole screenshot deal, but it's a nice thought. Use your imaginations.

GRAPHING THE NUMERICAL DERIVATIVE:

1. Input the funtion of which you wish to see the derivative into the Y1 entry line.
2. In the Y2 entry line, follow the following (teehee!) progression of buttons:
MATH
8
VARS
→Y-VARS
1
1
,
X
,
X
)
3. Now that you have punched this in, hit the ENTER button. On the resultant graph, you now have the original function and its derivative.
4. Note: When you see in the Y2 entry line “nDeriv(Y1,X,X)” I suppose you may want to know what this all means. This means you are finding the numerical derivative of the Y1 function for the variable X in terms of X. Instead of using nDeriv( to find an individual slope at a point, we are instead using it to graph the slopes of all tangent lines to the curve, THE DERIVATIVE!

INTERMEDIATE VALUE THEOREM

The Intermediate Value Theorem is stated as follows:

If a and b are any two values on a function, f, and f is differentiable then f’ takes on all values between f’(a) and f’(b).

As Marchetti said, that’s a lot of mathspeak, which is something most of us don’t understand. Basically, if a function is differentiable, then a tangent line exists at all points. If I’m wrong on that, then correct me. Basically, it says that if the function can have a derivative between a and b, then the function will.

Rates of Change:

There are two methods for finding Instantaneous RoC, finding the RoC for any point on the function, and finding the RoC at a specific point. Here they are:


Inst. RoC for a Function (Defn. of Derivative):

f'(x)=(f(x+h) - f(x))/h

Inst. RoC at a Point, “a”

f'(a)=(f(a+h) - f(a))/h

I think that’s about it, thank you all for your time and I apologize dearly for my lack of punctuality. The homework, in case you’re looking desperately at this, is pg 140 # 29, 28, 33, 31, and 32 (yes, in that order).

Ok, I'm encoding this post in HTML so let me know if there are any problems. I figure I can use some coding to slightly alter the color of the math portions, therefore making them easier to read. Alright, so here we go:

Graph of Y' Stuff

Graphs are pretty important in Calculus as they form an easy allabi when you can't solve a problem. Anyways, there are alot of sweet things to know about a graph for example, if we take the function F(x)=X² who's graph is


then you take the Derivative of the function, which happens to be Y' = 2X¹ and you get this



Now you'll notice several things right away. First, is that the degree of the function is one lower. Second, you'll also notice, and the zero of the derivative is at the minimum of the original function. This can clearly be seen when you graph both of them at the same time



and zoomed in



Example Graphs

I figure I'll use a list instead of a table, the blog site probably won't respond to the coding. The function is in black, whilst the derivative is in red. The original function will come first, then both of then together.

1. F(x)=sinX & Y'=cosX




2. F(x)=X³ + 2X² & Y'=3X² + 4X

So if we can take two rules from all of this:

1. If F(x) is a polynomial, than F'(x) will be one degree lower.


2. If F(x) is continuous and at a maximum or a minimum at A than F'(x) will be 0 at A.
   

Trig Tricks

Alright, even though Trigonometry is a total pain in the ass, we still have to do it. That being said, it's time consuming, stressful, and slightly annoying when you're attempting to find the F'(x) of a trig function. So, there are a couple tricks that make your life a whole lot easier when applied with the other calculus rules. On the left is a function, and on the right in green is the Y' of that function

• F(x)=sinX F'(x)=cosX


• F(x)=cosX F'(x)=-sinX


• F(x)=secX F'(x)=secXtanX


• F(x)=tanX F'(x)=sec²X



• F(x)=cscX F'(x)=-cscXcotX


• F(x)=cotX F'(x)=-csc²X

Below is an example problem of how to use these tricks along with the Quotient Rule:
Your starting function
Y=cosX / (1-sinX)
Apply the Quotient Rule
Y'= (1-sinX)(-sinX) - cosX(-cosX) / (1-sinX)²
Simplify by distributing
Y'=-sinX + sin²X + cos²X / (1 - sinX)²
Next use identies to turn the Sin²X into (1-cos²X) and subtract the cos²X
Y'= -sinX + 1 + - cos²X + cos²X / (1 - sinX)²
Now cancel out a (1 - sinX)
Y'= (1 + sinX) / (1 - sinX)²


Y'= 1 / (1 - sinX)

Alright, that's it

Dalton King